Тестирование функции minimum на «четырехведерной» задаче
Алгоритм спуска к минимуму, заложенный в программу на рис. 6.27, ¾ простой и без всяких оптимизирующих хитростей. Так, например, при очередном приближении к минимуму лишний раз рассчитывается значение анализируемой функции в предыдущей точке. Если анализируемая функция простая и ее значение высчитывается быстро, то это повторение мало влияет на общее время поиска минимума. Но что будет, если функция достаточно сложная? Предлагаем читателям доработать программу на рис. 6.27 и исправить отмеченный недостаток. Программа должна запоминать значение анализируемой функции в предыдущей точке приближения и использовать его в новом приближении. Это, кстати, заложено в метод золотого сечения (см. рис. 6.26). А вот более сложное задание. При поиске минимума функции двух переменных мы «перекрещиваем» точку очередного приближения, как бы благословляя успех поиска:
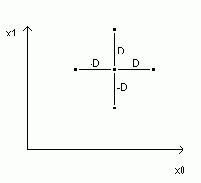
Более оптимальная стратегия может требовать «охвата» очередной точки не крестом, а равносторонним треугольником со стороной D (симплекс-метод; при минимизации функции трех переменных точка помещается внутри тетраэда и т. д.):
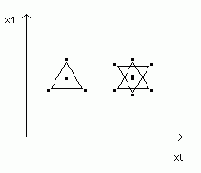
Кроме того, неплохо треугольник (либо звезду Давида или даже пятиконечную звезду – новое задание читателю) при каждом шаге приближения к минимуму ориентировать в пространстве случайным образом, растягивать его вдоль одной из вершин. Этим также можно добиться более оптимальной стратегии поиска минимума.
Описанные ухищрения можно перенести и на задачу с n переменными оптимизации (n-мерная иудейская или пятиконечная звезда!). Все это будет хорошим заданием читателям. Поиск и испытание алгоритмов оптимизации относится к одному из разделов вычислительной (прикладной) математики. В данной книге мы только чуть-чуть заглянули в него.
Читатель может отметить еще одну «неоптимальность» программы на рис. 6.27. Она генерирует не только вектор значений переменных, где функция минимальна, но и целую матрицу М с «историей» поиска, которую потом приходится транспортировать (МТ), определять номер ее последнего столбца (L) и вычленять его (М<L-1> – см. рис. 6.28). Но перегрузка программы на рис. 6.27 не была напрасна. Как уже отмечалось ранее, программирование в среде Mathcad лишено средств отладки. Простейшее, но тем не менее очень эффективное средство отладки программ – наблюдение за промежуточными результатами. А как раз это в среде Mathcad делать невозможно. И все же – если нельзя, но очень хочется, то можно. Программа, приведенная на рис. 6.27, успешно справляется с довольно-таки сложными задачами (см., например, рис. 6.28). Но если ей подсунуть совсем уж простую функцию – тестовую функцию Розенброка из этюда 3, то при определенных начальных приближениях программа на рис. 6.27 зациклится – ответа от нее не дождешься. В чем тут дело? Ответить на этот вопрос поможет некоторая модернизация программы: прервать ее работу можно не только по условию D £ TOL, но и по дополнительному условию, например, n > 30. После того как число шагов приближения n превысит 30, можно будет просмотреть след поиска минимума функции Розенброка или иной другой (задание читателю).