Разложение чисел на простые множители
На рис. 7.11 даны примеры работы оператора n factor ®. Если исходное число n простое, то система Mathcad довольно быстро (секунды, минуты) доказывает это и выдает один сомножитель – само исходное простое число. Короткие составные числа раскладываются на простые сомножители также за приемлемое время. Но если составное число удлинить, то Mathcad «задумывается» намертво. Не «зависает», а именно задумывается. Автор оставлял включенную машину на выходные: вместо курсора-стрелки появлялся курсор – докторская четырехуголка, что свидетельствовало о работе символьного процессора. В понедельник ответа не было, а после нажатия клавиши Esc, вызывающего диалоговое окно прерывания вычислительного процесса, и щелчку по кнопке OK работоспособность Mathcad восстанавливалась:
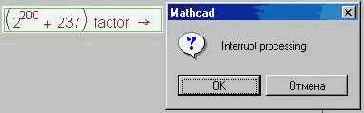
Простые числа на рис. 7.11 – это не просто простые числа, взятые наугад, а числа из различных литературных источников, где они отмечались как самые большие простые числа, известные человеку на определенных этапах развития математической науки и техники счета. Числа вида 2n-1 называют числами Мерсенна (http://www.mersenne.org). Они могут быть простыми лишь в том случае, если n – простое число (условие необходимое, но недостаточное – число 267-1 составное, хотя число 67 простое). До сих пор не доказано, имеется ли конечное или бесконечное число простых чисел Мерсенна[25]. То же можно сказать и в отношении простых чисел, состоящих только из единиц.
Особо хочется отметить число 2521-1. На рис. 7.11 показано, что это число Мерсенна – простое. Но в книге Мартина Гарднера (о ней ниже), сказано, что в 1982 году суперкомпьютер[26] «Крей» разложил его на три простых множителя за 32 часа работы. Где здесь ошибка? Либо Mathcad неправильно факторизирует числа, либо в книге Гарднера прошла опечатка (очепятка). Второе вероятнее, так как в книге отмечено, что это 69-значное число, тогда как на самом деле оно имеет больше знаков. Предлагаем читателю самому разобраться в этом вопросе. Автору тут важно поднять проблему и наметить пути ее решения с помощью Mathcad.
Для проверки чисел на простоту используют так называемую малую теорему Ферма[27] (см. пункт 2 на рис. 7.11). Если p – простое число, а число a – случайное, меньшее, чем p, то функция Ferma возвращает единицу. Если р – составное число, то функция Ferma возвращает число, большее единицы. И большая и малая теоремы Ферма пока считаются не доказанными, но если кандидат на простое число несколько раз выдерживает тест Ферма[28], то его считают «условно» простым и используют в шифровальном деле.
Я только что изложил главу «Надежные шрифты» из книги Мартина Гарднера «От мозаик Пенроуза к надежным шрифтам» (М.: Мир, 1993). После ее прочтения у меня возникло такое чувство, что либо я сам что-то недопонимаю, либо и меня и Гарднера кто-то искусно водит за нос, отвлекая от раскрытия настоящих алгоритмов шифрования.
Вот отрывок из этой книги.
«Объясняя, как работает их (шифровальная. – здесь и далее примечания автора) система, авторы из МТИ (Массачусетский технологический институт) выбрали в качестве исходного текста парафраз ремарки из «Юлия Цезаря» Шекспира (акт I, сцена 2): "ITS ALL GREEK ТО ME" («Для меня все это сущая тарабарщина» – мы говорим «китайская грамота», англичане же при этом вспоминают греков).
Прежде всего, этот текст преобразуется в одно большое число с помощью стандартного ключа: А=01, В=02, ..., Z=26 (00 – пробел между словами). Получается число 09201900011212000718050511002015001305.
Полученное число шифруется путем возведения его в s-ю степень по модулю некоторого составного числа r. Составное число r получается как произведение двух случайно выбранных простых чисел p и q, каждое из которых не менее чем 40-значно. Число s должно быть взаимно простым с числом p-1 и q-1. Числа s и r общедоступны: они используются в шифрующем алгоритме. Операция шифрования осуществляется весьма эффективно даже при очень больших значениях r; на практике она требует менее одной секунды компьютерного времени.
Два простых множителя числа r хранятся в памяти компьютера, поскольку они используются в секретном обратном алгоритме. Обратный алгоритм, используемый при дешифровке, состоит в возведении числа-шифротекста в другую степень t и в нахождении остатка от деления полученного числа на r, то есть в приведении по модулю r. Как и в предыдущем случае, на это уходит менее секунды машинного времени. Но показатель t может вычислить только тот, кто знает p и q ¾ два простых числа, которые хранятся в секрете.
Если исходный текст слишком велик для того, чтобы с ним можно было обращаться как с одним числом, то его следует разбить на блоки и каждый блок рассматривать как отдельное число. Я не буду вдаваться здесь в дальнейшие подробности. Они носят несколько технический характер и ясно изложены в отчете МТИ.
Для шифрования текста ITS ALL GREEK TO ME группа из МТИ выбрала s=9007 и r=114381625757888867669235779976146612010218296721242362562561842935706935245733897830597123563958705058989075147599290026879543541.
Число r есть произведение 64-значного простого числа p и 65-значного простого числа q, каждое из которых выбрано случайным образом. Шифрующий алгоритм заменяет число, соответствующее исходному тексту (09201...), следующим числом-шифротекстом: 199935131497805100452 31712274026064742320401705839146310370371740625971608948 927504399209626725826750128935544613538 23769748026.
Желая поощрить тех читателей журнала «Scientific American[29]», которые хотели бы испробовать свои силы на поприще криптоанализа, группа из МТИ зашифровала с помощью того же общедоступного алгоритма другой текст. Шифротекст вы видите на рис. 92 (см. книгу Гарднера). Его оригинал представляет собой предложение на английском языке. Сначала оригинальный текст был превращен в число с помощью стандартного метода, который был объяснен выше, полученное число возведено в 9007-ю степень (по модулю r) с помощью остроумного метода, изложенного в отчете. Тому, кто первым расшифрует текст, группа из МТИ обещала выплатить премию в 100 долларов.
Для доказательства того, что шифротекст действительно исходит от группы из МТИ, к нему была добавлена следующая подпись: 16717861150380844246015271389168398245436901032358311217835038446929062655448792237114490509578608 655662496577974840004057020373.
Подпись зашифрована с помощью секретного обратного шифрующего алгоритма. Так как читатель не располагает своим общедоступным шифрующим алгоритмом, вторая шифрующая операция была опущена. Каждый читатель, имеющий доступ к компьютеру и алгоритмам, опубликованным в отчете МТИ, может легко прочитать подпись с помощью общедоступных шифрующих алгоритмов группы МТИ, то есть возвести приведенное выше число в 9007-ю степень и перейти к остатку от деления на r.
Проделав эти операции, читатель получит число 06091819200019151222051800230914190015140500082114041805040004151212011819. Пользуясь стандартным ключом, читатель расшифровывает это число как FIRST SOLVER WINS ONE HUNDRED DOLLARS («первый, кто расшифрует текст, получит сто долларов»). Этот подписанный шифротекст мог быть получен только от группы из МТИ, так как обратный алгоритм, которым был зашифрован исходный текст, известен только членам этой группы.»
На этом заканчивается отрывок из книги Гарднера. Он сначала писался Гарднером по-английски, затем набирался в типографии, потом переводился на русский язык, опять набирался в типографии, затем сканировался автором для вставки в данную книгу. При такой технологии ошибки в числах текста очень вероятны. Тут вспоминается старая карикатура. Человек с перевязанными руками и ногами лежит на больничной койке, а диктор по телевизору, поставленному в палате, говорит: «Приносим извинения! В нашу вчерашнюю передачу «Делай с нами, делай как мы, делай лучше нас!» вкралась ошибка». Римейк карикатуры. «Пациент «палаты № 6» в книге по компьютерной математике читает приписку: «В наше предыдущее издание вкралась ошибка».
Автор перемножил в среде Mathcad[30]
два простых числа и поместил произведение в пункте 3 на рис. 7.1. Кто первым определит, что за простые числа были перемножены (найдет потайную кнопку шифра), получит приз, название которого также зашифровано: «Кмапвсптор к мвуепа»[31].
Оператор символьного преобразования с ключевым словом можно считать зачатком нового языка программирования, ориентированного не на вычислительный, а на аналитический процесс. Но интеграция символьной математики в среду Mathcad еще слаба и требует обилия ручной работы, без которой не составить даже функции пользователя из преобразованного выражения.
Один из коллег автора пришел в полный восторг, увидев действие пары expand – series. Ему (а он преподаватель математики в институте) по долгу службы приходится составлять вопросы для вступительных экзаменов. Ключевые слова expand – series позволяют как из рога изобилия сыпать вопросами с заголовком «Упростить», заранее имея правильный ответ. Несколько охладила этот восторг мысль о том, что абитуриенты пронесут
на экзамен ноутбук[32]
и ключевыми словами factor и simplify все эти примеры «разъяснят». Правда, на экзамене, как и в самом учебном процессе, требуется не столько ответ, сколько промежуточные выкладки... К проблеме щита и меча во взаимоотношениях ученика и учителя мы вернемся чуть позже, рассматривая место пакета Mathcad и ему подобных в процессе преподавания не только чисто технических дисциплин, но и самой высшей математики.
В среде Mathcad 8 можно вести цепочку символьных преобразований, показывая или не показывая промежуточные выкладки, которые иногда бывают настолько громоздкими, что их не то что рассмотреть – стереть с экрана бывает затруднительно.