Операторы и функции для работы с векторами и матрицами
Векторные и матричные операторы
Для работы с векторами и матрицами система MathCAD содержит ряд операторов и функций. Вначале рассмотрим операторы, введя следующие обозначения: для векторов — V, для матриц —Ми для скалярных величин — Z. Ниже представлены операторы для работы с векторами и матрицами:
| Оператор V1+ V2 VI-V2 -V
-м V-Z z* v, v* z Z* M, M* Z V1* V2 M* V M1* M2 V z M z м-1 M" IV] | Ввод
V1+ V2 V1-V2 -V -M V-Z z* v, v* z Z* M, M* Z V1* V2 M* V M1* M2 v/z M/Z ivr-i M^ IV | Назначение оператора
Сложение двух векторов VI и V2 Вычитание двух векторов VI и V2 Смена знака у элементов вектора V Смена знака у элементов матрицы Вычитание из вектора V скаляра Z Умножение вектора V на скаляр Z Умножение матрицы М на вектор Z Умножение двух векторов VI и V2 Умножение матрицы М на вектор V Умножение двух матриц Ml и М2 Деление вектора V на скаляр Z Деление матрицы М на скаляр Z Обращение матрицы М Возведение матрицы М в степень п Вычисление квадратного корня из ^V |
¦М¦ ¦М Вычисление определителя матрицы
VT V Ctrl! Транспонирование вектора V
МT М Ctrl! Транспонирование матрицы М
VlxV2 VI Ctrl * V2 Кросс-умножение двух векторов VI и V2
V V" Получение комплексно-сопряженного
вектора М М" Получение комплексно-сопряженной
матрицы ZV Alt $ V Вычисление суммы элементов вектора V
V V Ctrl - Векторизация вектора V
М М Ctrl - Векторизация матрицы М
М<n> М Ctrl л п Выделение п-го
столбца матрицы М
Vn V [ п Выделение п-го элемента вектора V
Мm,n М [(m,п) Выделение элемента (т,п) матрицы М
Следует отметить, что в некоторых операторах для ввода используется клавиша Ctrl, тогда как в ранних версиях системы MathCAD для этого предназначалась клавиша Alt (в последней версии Alt используется для начала активизации главною меню)
Операция векторизации
Большинство приведенных операторов достаточно известны из математического аппарата матричных вычислений. Под необычным для нашей математической литературы понятием "векторизация" подразумевается одновременное проведение математических операций в их скалярном значении над всеми элементами вектора или матрицы, помеченными знаками векторизации. Это можно понимать и как возможность параллельных вычислений.
Векторизация может изменить смысл математических выражений и даже превратить недопустимое выражение во вполне допустимое. Например, если V — вектор, то выражение cos(V) будет недопустимым, поскольку аргументом функции cos может быть только скалярная величина или переменная. Однако со знаком векторизации функция cos(V) возвращает вектор, каждый элемент которого есть косинус значения соответствующего исходного вектора V.
Если А и В — векторы, то
АЧВ дает скалярное произведение этих векторов. Но то же произведение под знаком векторизации создает новый вектор, каждый 7-й элемент которого есть произведение J-X элементов векторов А и В
Итак, векторизация позволяет использовать скалярные операторы и функции с массивами. Нередко это заметно упрощает запись математических алгоритмов, особенно для обеспечения параллельных вычислений. Впрочем, параллельность относится не к самим вычислениям, а лишь к их алгоритмической записи.
Векторные функции
Существует также ряд встроенных векторных и матричных функций. Они облегчают решение задач линейной алгебры и других сфер приложения векторов и матриц. Приведем векторные функции, входящие в систему MathCAD-
length(V) — возвращает длину вектора;
last(V) — возвращает индекс последнего элемента;
max(V) — возвращает максимальный по значению элемент;
min(V) —
возвращает минимальный по значению элемент;
Re(V) — возвращает вектор действительных частей вектора с комплекс ными элементами;
Im(V) — возвращает вектор мнимых частей вектора с комплексными элементами;
e(i,j, k) — полностью асимметричный тензор размерности три. г, j и k
должны быть целыми числами от 0 до 2 (или между ORIGIN и ORIGIN+2, если ORIGINS).
Результат равен 0, если любые два аргумента равны, 1 — если три аргумента являются четной перестановкой (0, 1, 2), и минус 1, если три аргумента являются перестановкой (0, 1, 2), кратной 2 и некратной 4.
Матричные функции
Для работы с матрицами также существует ряд встроенных функций. Они перечислены ниже:
augment(Ml,M2) — объединяет в одну матрицы Ml и М2, имеющие одинаковое число строк (объединение идет "бок о бок");
identity(n) — создает единичную квадратную матрицу размером п*п;
stack(Ml,M2) — объединяет две матрицы Ml и М2, имеющие одинаковое число столбцов, располагая Ml над М2;
submatrix(A,ir,jr,ic,jc) — возвращает субматрицу, состоящую из всех элементов, содержащихся в строках от ir no jr
и столбцов с ic по JC (irfjr и icfjc);
diag(V) — создает диагональную матрицу, элемент главной диагонали которой — вектор V;
matrix(ff2,n,f) — матрицу, в которой (i,j)-vi элемент содержит f(i,j), где г=0, 1,... т uj=0, 1,... п;
Re(M) — возвращает матрицу действительных частей матрицы М с комплексными элементами;
Im(M) — возвращает матрицу мнимых частей матрицы М с комплексными элементами.
Функции, возвращающие специальные характеристики матриц
Специальные характеристики матриц возвращаются следующими функциями:
cols(M) — возвращает число столбцов матрицы М;
rows(M) — возвращает число строк матрицы М;
rank(M) — возвращает ранг матрицы М;
tr(M) — возвращает след (сумму диагональных элементов) квадратной
матрицы М;
mean(M) — возвращает среднее значение элементов массива М;
median(M) — возвращает медиану элементов массива М;
condl(M) — возвращает число обусловленности матрицы, вычисленное в
норме L1;
cond2(M) — возвращает число обусловленности матрицы, вычисленное в
норме L2;
conde(M) — возвращает число обусловленности матрицы, вычисленное
в норме евклидова пространства;
condi(M) — возвращает число обусловленности матрицы, основанное на
равномерной норме;
norml(M) — возвращает L1, норму матрицы М;
norm2(M) — возвращает L2, норма матрицы М;
поппе(М) — возвращает евклидову норму матрицы М;
normi(M) — возвращает неопределенную норму матрицы М.
Примеры применения векторных и матричных операций
На рис. 11.12 приведены примеры использования наиболее распространенных векторных операторов, описанных выше.

Рис. 11.12 Применение операторов для работы с векторами
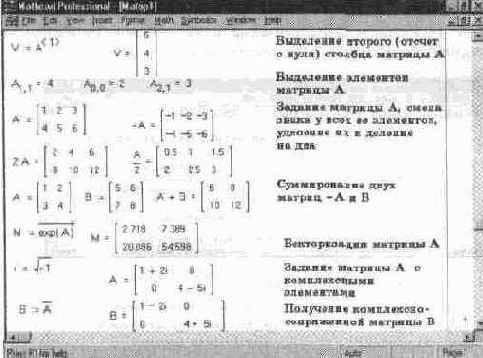
РИС.11.13 Примеры матричных операций (начало)

MathCAD делает работу с векторами и матрицами столь же простой, как и с обычными числами и переменными Это, безусловно, способствует проникновению векторных и матричных методов математических вычислений в практику научно-технических и иных расчетов
Применение операторов для работы с матрицами показано на рис 11 13 Поскольку не все матричные операции поместились в окне документа, представленного на рис 1113, конец документа с другими матричными операциями показан на рис 11 14
Рис. 11.14 Примеры матричных операций (конец)
На рис 1115 приведен ряд примеров применения наиболее распространенных матричных функций

Рис.11.15 Примеры применения матричных функций (начало)
Конец документа с примерами матричных функций показан на рис 11.16 Заметим, что раньше для задания таких функций приходилось готовить довольно сложные программы
Рис. 11.16 Примеры применения матричных функций (конец)

Дополнительные матричные функции
В профессиональные версии MathCAD включен ряд дополнительных матричных функций Они перечислены ниже.
eigenvals(M) — возвращает вектор, содержащий собственные значения матрицы М,
eigenvec(M,Z) для указанной матрицы М и заданного собственного значения Z возвращает принадлежащий этому собственному значению вектор,
eigenvecs(M) — возвращает матрицу, столбцами которой являются собственные векторы матрицы М (порядок расположения собственных векторов соответствует порядку собственных значений, возвращаемых функцией eigenvals),
genvals(M,N) — возвращает вектор обобщенных собственных значений v1 соответствующий решению уравнения M-x=v,-N-x (матрицы М и N должны быть вещественными),
genvals(M,N) — возвращает матрицу, столбцы которой содержат нормированные обобщенные собственные векторы,
Ф1и(М) — выполняет треугольное разложение матрицы М- P-M=L-U, L и U — соответственно нижняя и верхняя треугольные матрицы Все четыре матрицы квадратные, одного порядка;
Фqr(A) — дает разложение матрицы A, A=Q-R, где Q, — ортогональная матрица и R — верхняя треугольная матрица,
(Bsvd(A) — дает сингулярное разложение матрицы А размером n m A*S*VТ
где U и V — ортогональные матрицы размером m m и n n соответственно, S - диагональная матрица, на диагонали которой расположены сингулярные числа матрицы А,
Фsvds(A) — возвращает вектор, содержащий сингулярные числа матрицы А размером т-п, где т>п;
Egeninv(A) - возвращает матрицу левую обратную к матрице А.
L-A=E, где Е — единичная матрица размером п* п, L — прямоугольная матрица размером n-rn, A — прямоугольная матрица размером п*п.
Функции сортировки для векторов и матриц
Начиная с третьей версии в системе MathCAD появились некоторые дополнительные функции сортировки — перестановки элементов векторов и матриц:
sort(V) — сортировка элементов векторов в порядке возрастания их значений;
reverse(V) —
перестановка элементов (после sort) в обратном порядке;
csort(M,n) — перестановка строк матрицы М таким образом, чтобы отсортированным оказался п-й столбец;
rsort(M,n) — перестановка столбцов матрицы М таким образом, чтобы отсортированной оказалась п-я строка.
Примеры применения дополнительных векторных и матричных функций
На рис. 11.17 представлены примеры, иллюстрирующие работу некоторых дополнительных векторных и матричных функций.
Рис. 11.17 Работа дополнительных векторных и матричных функций

Решение систем линейных уравнений
В целом векторные и матричные операторы и функции системы MathCAD позволяют решать широкий круг задач линейной алгебры. К примеру, если задана матрица А и вектор В для системы линейных уравнений в матричной форме АхХ:=В, то вектор решения можно получить из очевидного выражения Х:=А-1*В. На рис. 11.18 приведен пример решения системы линейных уравнений.

Рис. 11.18 Решение системы линейных уравнений
Для решения систем линейных уравнений в MathCAD PLUS введена встроенная функция
Isolve(A.B),
которая возвращает вектор Х для системы линейных уравнений А-Х=В при заданной матрице коэффициентов А и векторе свободных членов В. Если уравнений п,
размерность вектора В должна быть п, а матрицы А — п-п. Пример применения этой функции также дан на рис. 11.18.