Функции для решения дифференциальных уравнений
Начиная с версии 5.0 в систему была введена возможность решения дифференциальных уравнений и систем с такими уравнениями в численном виде. Эту возможность трудно переоценить, так как многие серьезные научно-технические задачи (особенно относящиеся к анализу динамических систем и к их математическому моделированию) базируются на численных методах решения систем дифференциальных уравнений.
Нелинейные дифференциальные уравнения и системы с такими уравнениями, как правило, не имеют аналитических методов решения, и здесь особенно важна возможность их решения численными методами. В большинстве случаев желательно представление решений в графическом виде, что и позволяет MathCAD.
В прежних версиях MathCAD пользователю приходилось самостоятельно составлять документы с решением таких уравнений, например, методом Эйлера или Рунге — Кутта, что было делом не очень простым. К тому же решение загромождало текст документа. Теперь эта проблема решена, и довольно изящно.
Функции для решения обыкновенных дифференциальных уравнений
Для решения задач такого класса в MathCAD введен ряд функций. Вначале остановимся на функциях, дающих решения для систем обыкновенных дифференциальных уравнений:
rkadapt — возвращает матрицу, содержащую таблицу (у, х1, х2, асc, п,
F, k, s) значений решения задачи Коши на интервале от х1 до х2 для системы обыкновенных дифференциальных уравнений, вычисленную методом Рунге — Кутта с переменным шагом и начальными условиями в векторе у (правые части системы записаны в векторе F, n — число шагов, k — максимальное число промежуточных точек решения и s — минимально допустимый интервал между точками);
Rkadapt(y, х1, х2, п, F) — возвращает матрицу решений методом Рунге — Кутта с переменным шагом для системы обыкновенных дифференциальных уравнений с начальными условиями в векторе у, правые части которых записаны в символьном векторе F, на интервале от х1 до х2', п - число шагов;
rkfixed(y, х1, х2, п, F) — возвращает матрицу решений методом Рунге —
Кутта системы обыкновенных дифференциальных уравнений с начальными условиями в векторе у, правые части которых записаны в символьном векторе F, на интервале от х1 до х2 при фиксированном числе шагов п.
Рис. 11. 40 иллюстрирует технику решения системы из двух дифференциальных уравнений и построение решения в виде фазового портрета колебаний, которые описываются решением заданной системы уравнений.
Рис. 11.40 Решение системы дифференциальных уравнений с применением функции rkfixed
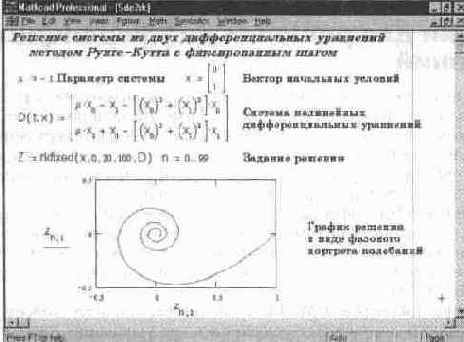
На рис. 11.41 показано решение той же системы с применением функции Rkadapt.
Обычно она, благодаря автоматическому изменению шага решения,
Рис. 11.41 Решение системы из двух дифференциальных уравнений с применением функции Rkadapt
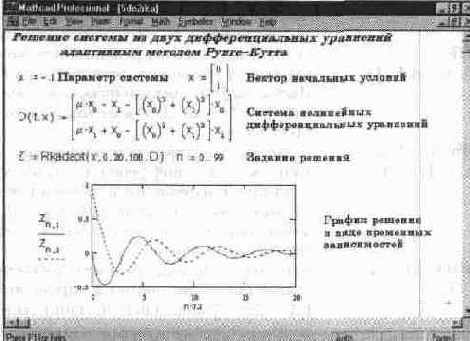
дает более точный результат. Естественно, по скорости вычислений она проигрывает функции rkfixed, хотя и не всегда: если решение меняется медленно, это может привести к заметному уменьшению числа шагов. Таким образом, функция Rkadapt наиболее привлекательна для решения систем дифференциальных уравнений, дающих медленно изменяющиеся решения.
В последнем примере решение представлено в виде временных зависимостей. Много других примеров решения дифференциальных уравнений можно найти в электронных книгах системы.
Если решение системы дифференциальных уравнений имеет вид гладких функций, то вместо функции rkfixed, описанной ранее, целесообразно применять новую функцию:
Bulstoer(y, x1, x2, n, F)
Она возвращает матрицу решения системы обыкновенных дифференциальных уравнений, правая часть которых (в виде первых производных неизвестных функций) записана в векторе F(x, у) при заданных в векторе у начальных условиях и при решении на интервале от x1
до x2 для n точек решения, не считая начальной точки. Вы можете заменить функцию Rkadapt в примере, показанном на рис. 11.40, на Bulstoer и опробовать последнюю в работе.
Функции для решения жестких систем дифференциальных уравнений
Система дифференциальных уравнений, записанная в матричной форме у=А-х,
где А — почти вырожденная матрица, называется жесткой. Для решения жестких дифференциальных уравнений в последние версии MathCAD введен ряд функций:
Фbulstoer (у, x1, x2, —
возвращает матрицу решения системы обыкновен-асс, n, F, k, s) ных дифференциальных уравнений, правая часть которых записана в символьном векторе F с заданными начальными условиями в векторе у, на интервале от x1 до x2.
Используется Bulirsch-Stoer-метод решения с переменным шагом. Параметры k и s задают максимальное
число промежуточных точек, на которых ищется решение и минимально допустимый интервал между ними;
Ф Stiffb — возвращает матрицу решений жесткого дифферен-(у, х1, х2, п, F, J) циального уравнения, записанного в F и функции
Якобиана J; у - вектор начальных значений на интервале от х1 до х2.
Для решения используется Bulirsch-Stoer-метод;
Ф stiffb (у, х1, х2, —
возвращает матрицу решений только в конечной асc, п, F, J, k, s) точке жесткого дифференциального уравнения, записанного в F и функции Якобиана J; у — вектор начальных значений на интервале от х1 до х2. Для решения используется метод Bulirsch-Stoer с переменным шагом;
Ф Stiffr(y, х1, х2, —
возвращает матрицу решений дифференциального п,
F, J) уравнения, записанного в F и функции Якобиана
J; у — вектор начальных значений на интервале от х1 до х2. Для решения используется метод Розенброка;
Ф stiffr(y, х1, х2, —
матрица решений только в конечной форме жест-асе,n, F, J, k, s) кого дифференциального уравнения, записанного в F и функции Якобиана J; у — вектор начальных значений на интервале от х1
до х2. Для решения используется метод Розенброка с переменным шагом. В приведенных функциях: асc — погрешность решения (рекомендуется порядка 0.001), k — максимальное число промежуточных точек ид— минимально допустимый интервал между точками, в которых ищется решение. Обратите внимание, что функции, начинающиеся со строчной буквы, дают решения только для конечной точки. Различаются функции также и методом решения.
Функции для решения дифференциальных уравнений Пуассона и Лапласа
Для решения дифференциальных уравнений Пуассона (в частных производных второго порядка) и уравнений Лапласа в систему введены следующие функции:
Фbvalfit(vl, v2, х1, х2, xi, —
устанавливает начальные условия для F, LI, L2, score)
краевой задачи, заданной в векторах F, vl и v2
на интервале от х1 до х2,
где решение известно в некоторой промежуточной точке xi;
Фге1ах(М1, М2, МЗ, — возвращает квадратную матрицу решения М4, М5,
A, U, г) уравнения Пуассона для спектрального радиуса г, Фmultigrid(M, п) —
возвращает матрицу решения уравнения Пуассона, у которого решение равно нулю на границах;
sbval(y, х1, х2, F, L.,score) — дает установку начальных условий для краевой задачи, определенной в символьном векторе F; вектор у — начальные условия на интервале от х1 до х2.
Функции для решения краевых задач
Для решения двухточечных краевых задач предназначены функции
shval(v^c1,x2,D,load,score)
bvalfit(vl,v2,x1,x2,xf,S,loadl,load2,score)
В них векторы v, vl, v2 задают начальные условия; х, х1, х2 — граничные точки интервала решений; D(х,у) — функция, возвращающая п-компонент-ный вектор с первыми производными неизвестных функций, \oad(x1,v), \oadi(x1,vi), load2(;c2,v2) — векторзначные функции, возвращающие значения начальных условий в точках х1 (х2); score(xf,y) — векторзначная функция, возвращающая п-элементный вектор соответствия. Вектор указывает, насколько значения решений, начинающихся из точек х1 и х2, должны соответствовать xf. Например, если нужно совпадение решений, то score(xf, у):=у.
Большое число примеров на решение дифференциальных уравнений с описанными функциями дается в подсказках QuickSheets, размещенных в центре ресурсов.