Решение задач фильтрации
Фильтрация аналоговых сигналов
Под фильтрацией подразумевается выделение полезного сигнала из его смеси с мешающим сигналом — шумов. Наиболее распространенный тип фильтрации — частотная фильтрация. Если известна область частот, занимаемая полезным сигналом, достаточно выделить ее и подавить те области, которые заняты шумом.
Документ на рис. 14. 27 иллюстрирует технику фильтрации с применением БПФ. В начале документа синтезируется двухчастотный сигнал, пред-
Рис. 14. 27 Фильтрация аналогового сигнала с применением БПФ (начало документа)
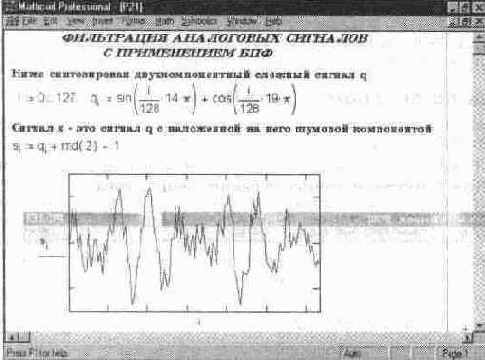
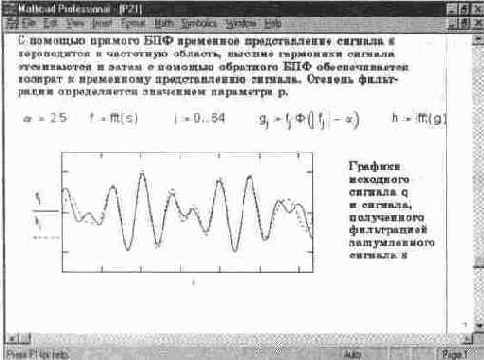
Рис. 14. 28 Фильтрация аналогового сигнала с применением БПФ (конец документа)
ставленный 128 отсчетами вектора q. Затем к этому сигналу присоединяется шум с помощью генератора случайных чисел и формируется вектор из 128 отсчетов зашумленного сигнала. Используя прямое БПФ, сигнал с шумом преобразуется из временной области в частотную, которую создает вектор f из 64 частотных составляющих. Затем выполняется фильтрующее преобразование, эффективность которого оценивается параметром фильтрации а. Отфильтрованный сигнал (вектор g) подвергается обратному БПФ и создает вектор выходного сигнала h.
В конце документа (см. рис. 14. 28) сравниваются временные зависимости входного и выходного сигналов. Хотя абсолютной идентичности между ними нет, видно, что выходной сигнал почти повторяет входной и в значительной мере избавлен от высокочастотных шумовых помех, маскирующих полезный сигнал.
Алгоритмы, реализованные в данном примере, находят широкое применение на практике. Они лежат в основе создания фильтров для аналоговых сигналов.
Цифровая фильтрация с помощью БПФ
Аналоговые фильтры обычно имеют довольно сложную аппаратную реализацию. В них применяются громоздкие и нетехнологичные колебательные контуры или RC-цепи с интегральными операционными усилителями. Поэтому интенсивно развивается новый класс фильтрующих устройств — цифровые фильтры. В них используются цифровые логические схемы, имеющие высокую степень интеграции, и применяются цифровые методы обработки сигналов.
Документ на рис. 14. 29 поясняет реализацию алгоритмов цифровой фильтрации с помощью реализуемой цифровыми устройствами функции s (kj). После ее определения синтезируется цифровой сигнал, содержащий низкочастотную в виде перепада и высокочастотную в виде меандра компоненты.
Далее показана реализация фильтрующей операции — свертки для двух типов фильтров, широкополосного и узкополосного. Конец документа, представленного на рис. 14. 29, показан на рис. 14. 30.

Рис. 14. 29 Реализация цифровой фильтрации (начало документа)

Рис. 14. 30 Реализация цифровой фильтрации (конец документа)
Заметим, что в данном примере речь идет не о фильтрации сигнала на фоне шумов, а о прохождении сложного составного сигнала через цифровые фильтры. Графики в конце документа иллюстрируют характер искажений сигнала при этом.
Фильтрация пространственного образа с применением двумерного БПФ
До сих пор мы приводили примеры применения одномерного БПФ. Однако возможно и двумерное преобразование Фурье, позволяющее решать более сложные задачи.

Рис. 14. 31 Фильтрация пространственного образа (начало документа)
Система MathCAD 7. 0 реализует двумерное БПФ, если в операциях БПФ использовать не векторы, а матрицы. Однако у ранних версий MathCAD таких возможностей нет. Поэтому воспользуемся более наглядной реализацией двумерного БПФ с помощью одномерного. На рис. 14.
31 показан документ, реализующий фильтрацию трехмерной поверхности с помощью двумерного БПФ.
В начале документа создается матрица трехмерной поверхности М со случайными отклонениями каждой точки. Внизу слева построена эта поверхность — см. рис. 14. 32. Она имеет вид пятна, в котором отдаленно угадываются общие контуры поверхности. Регулярность расположения точек-крестиков на ней вообще не заметна. В средней части документа показана реализация математического аппарата фильтрации. Рисунок справа внизу документа показывает результат фильтрации. На нем отчетливо видны не только общие формы поверхности (типа "выпуклый лист"), но и явная регулярность расположения точек. Это и есть результат фильтрации.
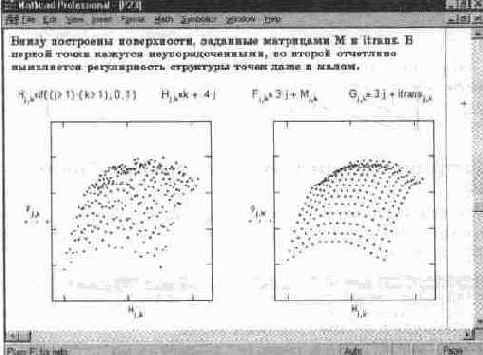
Рис. 14. 32 Фильтрация пространственного образа (конец документа)
Полезно отметить, что графики трехмерной поверхности здесь также получены без применения стандартных средств построения трехмерных поверхностей системы. Поэтому без какой-либо доработки (кроме выбора шрифта комментариев) этот пример можно использовать и в ранних версиях системы MathCAD 2. 0/2. 04, не имеющих средств построения трехмерных фигур (а говоря точнее, он и взят из примеров для этих систем).