Физические расчеты
Преодоление самолетом звукового барьера
Большинство из нас слышали в ясную погоду звуки, напоминающие гром. Почти наверняка это были либо отзвуки дальней грозы, либо грохот, создаваемый самолетом при преодолении звукового барьера. В физике известна функция М (и, h), определяющая так называемое число Маха, зависящее от скорости самолета и и высоты полета h [32]. В момент преодоления звукового барьера значение М (и, h)
становится равным 1. Скорость, на которой преодолевается этот барьер, падает с увеличением высоты полета.
Документ на рис. 14. 33 содержит определение функции М (и, h). На верхнем графике показаны зависимости М (и, h) от и для четырех значений h, а также уровень единицы. Звуковой барьер преодолевается в момент, когда соответствующая зависимости М (и, h)
кривая пересекает уровень единицы.
Рис. 14. 33 Расчет скорости преодоления самолетом звукового барьера (начало документа)
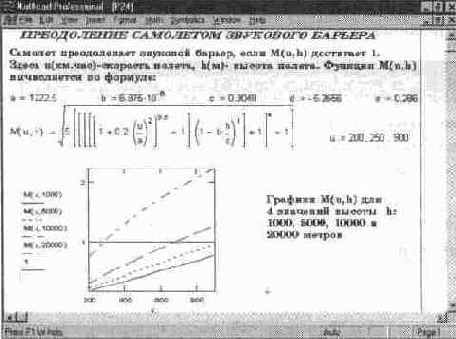
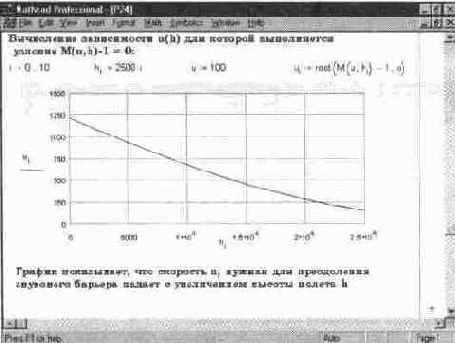
Рис. 14. 34 Расчет скорости преодоления самолетом звукового барьера (конец документа)
Более полезно не просто знать саму по себе зависимость М (и, h), а из условия М (и, h) =i получить зависимость скорости преодоления звукового барьера u (h) от высоты h. Для этого можно воспользоваться функцией поиска корня указанного условия. Это также сделано в конце документа (см. рис. 14. 34).
Этот пример дает наглядное представление о решении простых физичес ких задач, базирующихся на уравнениях теоретической физики, и демонстриру ет возможность находить с помощью MathCAD корень нелинейных уравнений
Потеря автомобилем энергии при торможении
Услышав визг тормозов автомобиля, мы с ужасом следим, сумеет ли он сбросить скорость и не настигнет ли нас до того, как мы успеем отскочить Полезно (скорее шоферу, чем нам) знать, как быстро автомобиль теряет энергию при торможении Решение этой задачи для автомобиля с дисковым тормозным устройством представлено на рис 14 35

Рис. 14. 35 Расчет потери энергии тормозящим автомобилем (начало документа)
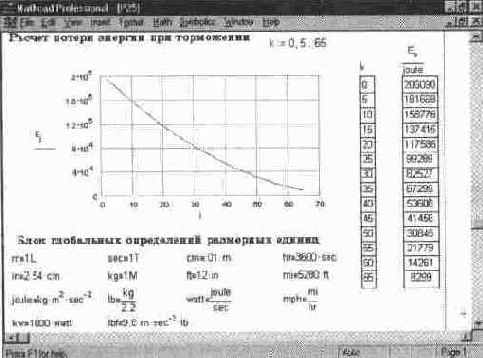
Рис. 14. 36 Расчет потери энергии тормозящим автомобилем (конец документа)
Процесс потери энергии в общем случае связан с решением нелинейного дифференциального уравнения. Физики любят использовать для такого решения простые конечно-разностные методы, при которых решение выражается рекуррентной формулой. Фактически эти методы соответствуют решению простым методом Эйлера. Результаты решения представлены на рис. 14. 36.
Важно отметить, что в данном расчете используются размерные величины (энергия определяется в джоулях). Для расчетов с размерными величинами в состав MathCAD входят файлы, содержащие глобальные определения этих величин. В конце документа (на рис 14. 36) показан пример использования такого файла. В нем содержится определение многих размерных величин, относящихся к физике (их больше, чем это нужно для нашего конкретного примера).
Расчет движения снаряда
Пусть спортсмен мечет снаряд (например, диск или ядро) с некоторой начальной скоростью VO и под углом Q к горизонту. По какой траектории происходит полет снаряда, если пренебречь сопротивлением воздуха? Ответ общеизвестен — по параболической Однако мы попытаемся ответить на этот вопрос моделированием движения, решая систему описывающих его дифференциальных уравнений численным методом Эйлера Этот подход иллюстрирует документ на рис. 14. 37.
Рис. 14. 37 Расчет траектории и угла наклона летящего снаряда
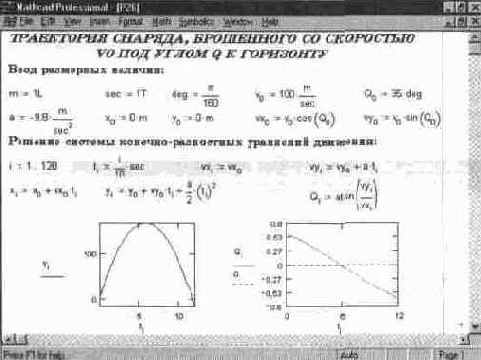
Обратите внимание, что операции (как это принято в физических расче тах) происходят с размерными величинами. В результате моделирования получены траектория движения снаряда (зависимость высоты от расстояния по горизонтали), а также зависимость угла наклона траектории от расстояния по горизонтали. Как и следовало ожидать, траектория полета снаряда оказалась параболической.
Падение парашютиста \
Рассмотрим существенно более сложный случай динамического движения:
на высоте уО из самолета выпрыгивает парашютист и в свободном полете падает вниз. Спустя пять секунд он дергает кольцо и испытывает заметные перегрузки из-за раскрытия парашюта и резкого снижения скорости падения. Моделирование падения основывается на решении нелинейной системы
Рис. 14. 38 Моделирование падения парашютиста (начало документа)

дифференциальных уравнений и требует учета сопротивления воздушной среды до и после открытия парашюта. В документе на рис. 14. 38 показано выполнение этого моделирования с применением конечно-разностного метода решения.
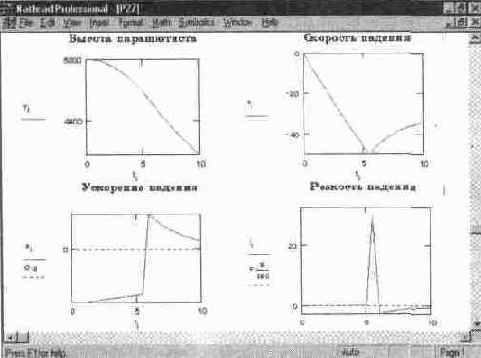
Рис. 14. 39 Данные о падении парашютиста (конец документа, представленного на рис. 14. 38)
В результате моделирования получены зависимости от времени падения парашютиста следующих параметров (см. рис 14 39): высоты, скорости и ускорения падения и резкости (второй производной от скорости) падения. Резкость падения характеризуют перегрузки, которые испытывает парашютист в полете Они многократно возрастают сразу после раскрытия парашюта
Если вас интересуют числовые данные величин, характеризующих падение парашютиста, выведите их в табличной форме.
