Электро- и радиотехнические расчеты
Электро- и радиотехнические расчеты — весьма благодатная почва для приложения MathCAD. Некоторые из таких расчетов (например, вычисление емкости или индуктивности различных компонентов) достаточно просты и сводятся (за редкими исключениями) к вычислениям по готовым формулам
В электро- и радиотехнике широко применяются комплексные числа и величины MathCAD обладает всеми возможностями для работы с ними, начиная от вычислений импеданса (полного сопротивления) простых цепей и кончая работой с матрицами, имеющими комплексные элементы
Ниже рассмотрено лишь несколько примеров расчетов электро- и радиотехнических цепей
Вычисление характеристик системы по ее операторной функции
Если схема описана операторной функцией, по ней можно вычислить важнейшие характеристики линейной системы. АЧХ, ФЧХ и переходную характеристику (т е. реакцию системы во времени на единичный скачок напряжения или тока на ее входе) Для вычисления АЧХ и ФЧХ достаточно заменить оператор p на величину iw, тогда модуль полученного выражения будет описывать АЧХ, а аргумент — ФЧХ
Построение АЧХ и ФЧХ для системы второго порядка, описанной операторной функцией, дано в документе на рис 14 40.
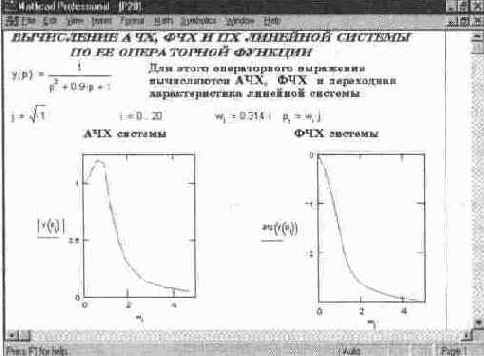
Рис. 14. 40 Построение АЧХ и ФЧХ линейной системы по ее операторной характеристике (начало документа)
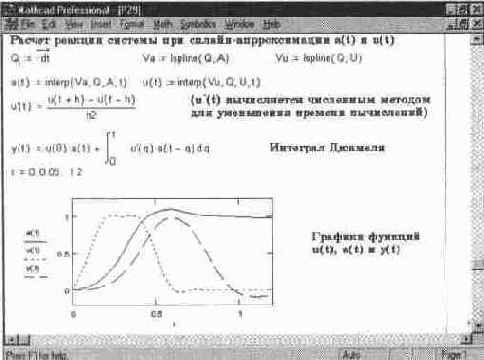
В этом документе представлено также построение по операторной функции передаточной характеристики системы. Для каждого значения времени t эта характеристика определяется интегралом с бесконечным пределом интегрирования:
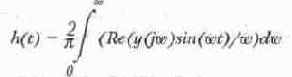
На рис. 14, 41 показано построение переходной характеристики.
Рис. 14. 41 Построение переходной характеристики (конец документа, представленного на рис. 14. 40)
К счастью, у всех реальных систем АЧХ на высоких частотах имеет спад и при больших w>wmax принимает близкие к нулю значения. В нашем примере это происходит уже при w>5,
что позволяет заменить бесконечный предел интегрирования на конечный.
Вычисление h (t) в документе на рис. 14. 42 выполнено по этому алгоритму. Число 0. 637 перед знаком интеграла есть значение 2/тс. Рядом с графиком h (t) выведена таблица времен t
и значений h (t). Анализируемая цепь является цепью 2-го порядка и имеет соответствующие признаки заметно демпфированной цепи 2-го порядка — характерный подъем АЧХ на некоторой частоте и переходную характеристику с небольшим выбросом.
Расчет отклика системы на воздействие, заданное таблично
Расчет отклика линейной системы с произвольной формой переходной характеристики на произвольно заданное входное воздействие — задача достаточно сложная. Ее решение облегчается, если передаточная характеристика и входное воздействие заданы в табличном виде, т. е. в виде ряда значений a (t) и u (t) для фиксированных моментов времени t на отрезке Т.
Наличие в системе MathCAD эффективного аппарата сплайн-интерполяции табличных данных позволяет с блеском решить такую задачу.
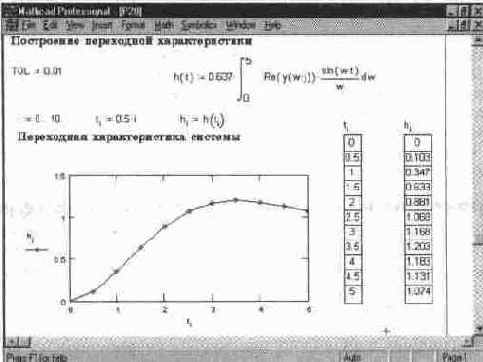
Документ на рис. 14. 42 иллюстрирует сказанное. Векторы А и U в нем задают узловые точки зависимостей a (t) и u (t) на отрезке времени Т. Эти векторы должны быть одинаковой длины, а их элементы должны относиться к соответствующим одинаковым моментам времени. Далее проводится сплайн-интерполяция (с линейной экстраполяцией) зависимостей aft) и u(t), что позволяет получить эти зависимости в непрерывном виде и использовать в интеграле свертки для вычисления реакции y (t).
Рис. 14. 42 Расчет реакции системы на заданное воздействие Сначапо документа)

Табличное задание u (t)
облегчает вычисление производной i/(t) в численном виде, что, в свою очередь, ускоряет вычисления. Обратите внимание, что здесь и' —
имя функции пользователя, вычисляющей значение производной численным методом. В конце документа (см рис. 14. 43) построены графические зависимости aft), u (t) и y (t).
Рис. 14. 43 Расчет реакции системы на заданное воздействие (конец документа)
Моделирование генератора гармонических колебаний на туннельном диоде
Пусть туннельный диод подключен к источнику постоянного напряжения Е через последовательно соединенные резистор R
и индуктор L. Пусть далее R и Е выбраны так, что рабочая точка туннельного диода находится на падающем участке N-образной ВАХ туннельного диода. Это обстоятельство принципиально важно, поскольку дифференциальная малосигнальная проводимость туннельного диода тогда является отрицательной. Физически это означает, что туннельный диод отдает энергию во внешнюю цепь.
Если учесть емкость С
туннельного диода (совместно с емкостью монтажа и нагрузочной емкостью), такая схема будет описываться следующей системой нелинейных дифференциальных уравнений [6, 8]:
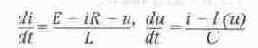
Нелинейность этой системы обусловлена тем, что во втором уравнении ток туннельного диода 1 (и) нелинейно зависит от напряжения на нем и емкости С. Зависимость 1 (и) есть N-образная вольт-амперная характеристика туннельного диода.
Документ на рис. 14. 44 позволяет рассчитать переходные процессы при включении рассмотренной схемы таблично заданной JV-образной ВАХ туннельного диода. Она задается своими табличными значениями — элементами векторов U и I. N-образная ВАХ получается сплайн-интерполяцией с кубической экстраполяцией Решение системы дифференциальных уравнений обеспечивается методом Эйлера

Рис. 14. 44 Моделирование генератора на туннельном диоде (начало документа)
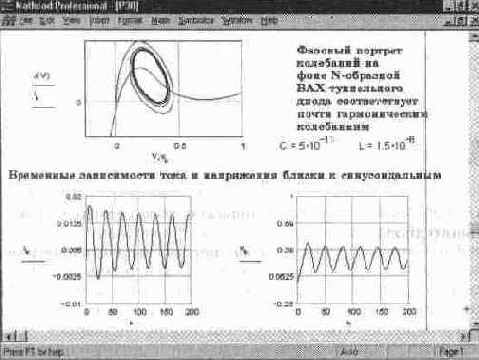
Результаты моделирования (см рис 14 45) в этом документе представлены в двух формах Первая имеет вид фазового портрета — положение каждой точки решения отмечается на графике в плоскости ВАХ Для чисто гармонических колебаний предельный цикл колебаний на фазовой плоскости должен иметь форму эллипса Его отличие от эллипса небольшое, что, с одной стороны, говорит о заметном влиянии нелинейности, а с другой — о почти гармоническом характере колебаний Вторая форма — временные зависимости напряжения на туннельном диоде и тока в цепи резистора R Эти зависимости близки к гармоническим
Рис. 14. 45 Моделирование генератора на туннельном диоде (конец документа)
Следует отметить, что область применения описанного документа неизмеримо шире, чем моделирование конкретной схемы генератора на туннельном диоде Практически с его помощью можно моделировать основную цепь на любом приборе с N- или N-образной ВАХ (например, индуктивный релак сатор на лавинном транзисторе, генераторы на N- и Л-диодах и транзисторах, их аналогах и т д) Достаточно лишь задать данные их ВАХ и соответствующие исходные данные
Стоит, к примеру, уменьшить емкость С в два-три раза, а индуктивность увеличить, как генератор перейдет в режим генерации релаксационных коле баний Этот случай показан на рис 14 46
Теперь возникают более резкие колебания, фазовый портрет начинается сразу с предельного цикла, форма которого принципиально отличается от эллиптической Соответственно, сильно отличаются от гармонической и форма напряжения на туннельном диоде, и форма тока, текущего через резистор R Колебания при этом относятся к типу релаксационных и возникают сами по себе, без какого-либо внешнего воздействия Практически после первого цикла колебаний устанавливается их стационарный режим
Еще более интересные результаты можно получить, используя импульсное питание цепи на туннельном диоде Тут напряжение питания можно задать зависимостью ei (t) в виде прямоугольно! о импульса, наложенного на постоянное напряжение — пьедестал. Напряжение выбирается так, что рабочая точка попадает на первую восходящую ветвь N-образной ВАХ и оказывается стабильной. При этом цепь устойчива и колебания не генерируются. При появлении импульса рабочая точка попадает на падающий участок и развивается процесс генерации одного полного цикла колебаний. Цепь, таким образом, выполняет функции ждущего релаксационного генератора. Читатель может самостоятельно изменить документ для реализации этого режима работы.
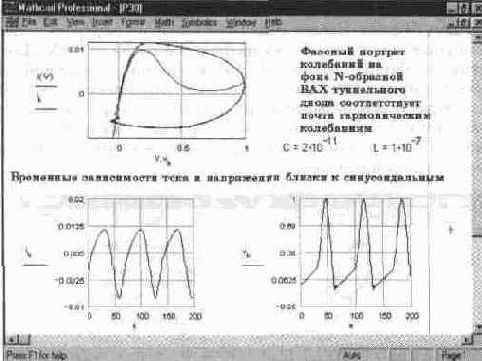
Рис. 14. 46 Пример генерации релаксационных колебаний
Приведенные выше примеры наглядно показывают, что даже незначительное изменение параметров одной и той же цепи на туннельном диоде способно резко (и даже качественно) изменить режимы ее работы. При этом цепь может выполнять практически любую функцию электронного устройства: нелинейного преобразователя, усилителя и генератора гармонических колебаний, автоколебательного и ждущего релаксатора и триггера.