Фазовый портрет полученный bulstoer (a) и rkadapt (б) (продолжение листинга 9 5)
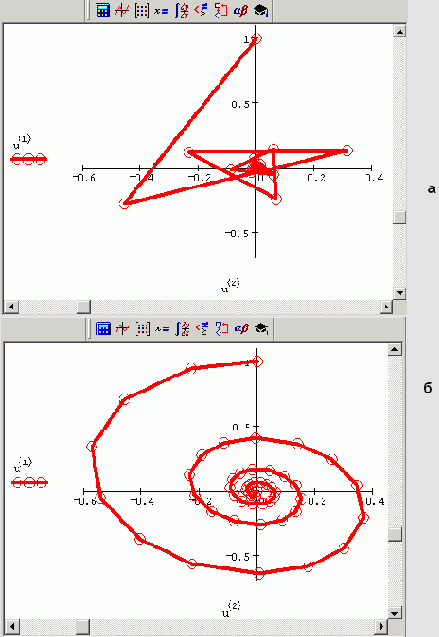
Рисунок 9.10. Фазовый портрет, полученный bulstoer (a) и rkadapt (б) (продолжение листинга 9.5)
Поэтому для экономии времени расчетов в функции buistoer можно выбирать и большие асе.
Чтобы обеспечить заданную точность, данные алгоритмы могут изменять как количество шагов, разбивающих интервал (t0,t1), так и их расположение вдоль интервала. Чтобы выяснить, на сколько шагов разбивался интервал при расчетах, воспользуемся простой программой, представленной в листинге 9.7. В ней определены пользовательские функции R(е) и B(е), вычисляющие для конкретной задачи (методов Рунге—Кутты и Булирша—Штера соответственно) зависимость числа шагов (т. е. числа строк получающейся матрицы) от параметра е=асс. Графики функций R(e) и B(е) показаны на Рисунок 9.11. Как видно, методу Рунге—Кутты при увеличении требуемой точности требуется все возрастающее количество шагов (и, соответственно, времени на расчеты), в противоположность методу Булирша—Штера, демонстрирующему большую экономичность.
Примечание 1
Примечание 1
Максимальное количество шагов алгоритма ограничивается еще одним параметром k встроенных функций buistoer и rkadapt (с/и. рази 9.3.3).