График решения (слева) и фазовый
Рисунок 9.17. График решения (слева) и фазовый портрет (справа) системы "хищник—жертва" (продолжение листинга 9.13)
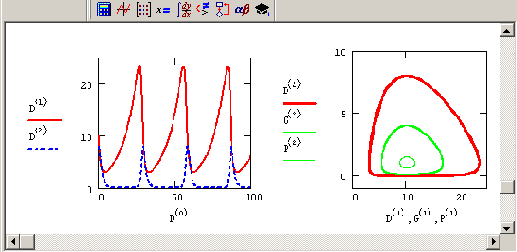
Рассмотренную модель динамики двух популяций легко можно модифицировать, изменив тип взаимодействия "хищник—жертва" на тип конкуренции. Для этого надо учесть, что рост численности каждой популяции тормозит, во-первых, межвидовая, и, во-вторых, внутривидовая конкуренция.
В результате система (во второй строке листинга) запишется в виде:
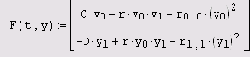
где матрица г задает коэффициенты убывания численности вследствие конкурентной борьбы (диагональные элементы соответствуют внутри-, а недиагональные — межвидовой конкуренции).
График решения (для разных начальных условий) и фазовый портрет для описанной системы ОДУ показаны на Рисунок 9.18. Как видно, конкурентная борьба приводит к установлению некоторого стационарного состояния, выражающего равновесие видов. Особая точка, к которой стремится решение системы ОДУ подобным образом, называется узлом.
Примечание 2
Примечание 2
Соответствующий файл с программой вы найдете на компакт-диске, вместе с более простой моделью динамики одной популяции с внутривидовой конкуренцией (называемой логистической моделью).