Неверное решение более жесткого ОДУ методом Рунге—Кутты (листин 9 8 с коэффициентом 50)
Рисунок 9.13. Неверное решение более жесткого ОДУ методом Рунге—Кутты (листин 9.8 с коэффициентом -50)
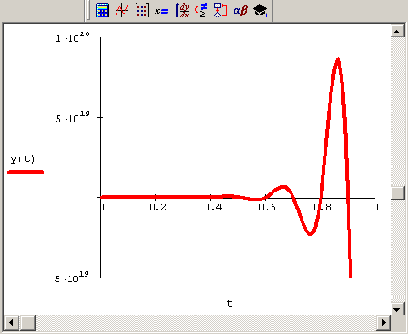
Таким образом, во-первых, мы выяснили, что одни и те же уравнения с разными параметрами могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примером ОДУ из листинга 9.8 все получилось хорошо, т. к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Для решения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.
Примечание 1
Примечание 1
Некоторые ученые замечают, что в последние годы методы Рунге—Кутты, считавшиеся ранее незыблемыми, стали уступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.