О постановке задачи
10.5.1. О постановке задачи
На примере решения нелинейной задачи взаимодействия световых пучков при помощи алгоритма стрельбы разберемся с физикой явления, которую описывает нелинейность. Рассмотрим простейшее усложнение модели (10.1) (см. разд. 10.1), добавив в уравнения малые слагаемые, зависящие квадратично от интенсивности света. Чтобы быть ближе к физической сущности явления, мы введем эту зависимость в формулу коэффициента поглощения среды а(х), сделав а(х) из (10.1) функцией не только координаты, но и суммарной интенсивности:
a(x,Y,y)=a0(x)-?(x)(Y+y), (10.8)
где а0(х) — постоянная (не зависящая от интенсивности света) составляющая коэффициента поглощения, а е(х) — малый коэффициент пропорциональности. В этом случае модель (10.1) перепишется в виде:
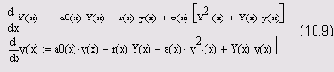
Таким образом, физическая подоплека квадратичной нелинейности задачи (10.9) связана с зависимостью коэффициента поглощения среды от Y+y. Иными словами, чем мощнее свет в некоторой точке среды, тем меньше локальный коэффициент поглощения среды в этой точке.
Механизм этого явления будет хорошо понятен, если предположить, что средой является воздух, насыщенный парами жидкости (попросту говоря, туман). Чем сильнее в некоторой точке туман, тем больше локальное поглощение. Если свет, проходящий через туман, имеет малую интенсивность, то он не оказывает на среду никакого (или почти никакого) воздействия. Однако если пучок света будет очень мощным, за счет его поглощения пары воды будут разогреваться и, следовательно, испаряться. По мере испарения капель воды туман станет рассеиваться, и среда просветлеет (т. е. ее коэффициент поглощения уменьшится). Таким образом, чем мощнее свет, тем активнее пойдет процесс испарения, тем существеннее уменьшится коэффициент поглощения. Именно такой эффект, совершенно понятный с физической точки зрения, и описывает формула (10.8) и, соответственно, модель (10.9).
Подчеркнем еще раз и физический смысл коэффициентов а0(х) и ?(х). Первый описывает постоянный (не зависящий от интенсивности света) коэффициент поглощения среды, а второй — его зависимость от эффекта разогрева среды светом. Чем больше коэффициент а0(х), тем более жесткой является краевая задача; а чем больше ?(х), тем сильнее ее нелинейность. В предельном случае ?(х)->0 задача (10.9) переходит в задачу (10.1), становясь линейной.