Решение задачи о собственных колебаниях струны
Листинг 10.5. Решение задачи о собственных колебаниях струны
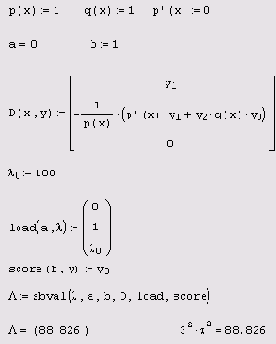
В первых двух строках листинга определяются функции, входящие в задачу, в том числе р' (х) :=0, и границы расчетного интервала (0,1). В третьей строке дается начальное приближение к собственному значению ?0, в четвертой вводится система ОДУ. Обратите внимание, что она состоит не из двух, а из трех уравнений. Первые два из них определяют эквивалентную (10.3) систему ОДУ первого порядка, а третье необходимо для задания собственного значения в виде еще одного компонента у2 искомого вектора у. Поскольку по определению собственное значение постоянно при всех х, то его производная должна быть приравнена нулю, что отражено в последнем уравнении. Важно также, что во втором из уравнений собственное значение записано как у2, поскольку является одним из неизвестных.
В следующих двух строках листинга задается левое граничное условие, включающее и недостающее условие на собственное значение для третьего уравнения, и правое граничное условие у0=0. В предпоследней строке листинга обычным образом применяется функция sbval, а в последней выводится результат ее работы вместе с известным аналитически собственным значением п2-я2. Как легко убедиться, мы нашли первое собственное значение для n=1, а чтобы найти другие собственные значения, необходимо задать другие начальные приближения к ним (в третьей строке листинга 10.5). Например, выбор ?0=50 приводит ко второму собственному значению 22?2, а ?0=100 — к третьему 32?2.
Чтобы построить график соответствующей собственной функции, надо добавить в листинг строку, программирующую решение задачи Коши, например, такую: u:=rkfixed(load(a,A) ,а,b, 100,D) . Полученные кривые показаны на Рисунок 10.6 в виде коллажа трех графиков, рассчитанных для трех собственных значений.
Примечание 1
Примечание 1
Примеры решения нескольких задач на собственные значения можно найти в различных Ресурсах Mathcad.