Эллиптические уравнения
11.3.2. Эллиптические уравнения
Решение эллиптических уравнений в частных производных реализовано только для единственного типа задач — двумерного уравнения Пуассона.
Это уравнение содержит вторые производные функции u(х,у) по двум пространственным переменным;
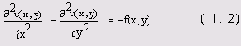
Уравнение Пуассона описывает, например, распределение электростатического поля u(х,у) в двумерной области с плотностью заряда f (x,y), или (см. разд. 11.1.2) стационарное распределение температуры u(х,у) на плоскости, в которой имеются источники (или поглотители) тепла с интенсивностью f (х,у) .
Примечание 1
Примечание 1
Несмотря на то, что применение встроенных функций, описанных в данном разделе, анонсировано разработчиками Mathcad только для уравнения Пуассона, их можно применять и для решения других уравнений, даже необязательно эллиптического типа. О том, как осуществить такие расчеты, написано в конце данного раздела.
Уравнение Пуассона с нулевыми граничными условиями
Корректная постановка краевой задачи для уравнения Пуассона требует задания граничных условий. В Mathcad решение ищется на плоской квадратной области, состоящей из (M+1)х(M+1) точек. Поэтому граничные условия должны быть определены пользователем для всех четырех сторон упомянутого квадрата. Самый простой вариант — это нулевые граничные условия, т. е. постоянная температура по всему периметру расчетной области. В таком случае можно использовать встроенную функцию multigrid:
- multigrid(F,ncycie) — матрица решения уравнения Пуассона размера (м+1)х(м+1) на квадратной области с нулевыми граничными условиями:
- F — матрица размера (M+1)х(M+1), задающая правую часть уравнения Пуассона;
- ncycle — параметр численного алгоритма (количество циклов в пределах каждой итерации).
ВНИМАНИЕ!
Сторона квадрата расчетной области должна включать точно N=2n шагов, т. е. 2n+1 узлов, где n — целое число.
Параметр численного метода ncycle в большинстве случаев достаточно взять равным 2.