Решение стационарного двумерного уравнения теплопроводности (см листинг 11 7 ниже)
Рисунок 11.2. Решение стационарного двумерного уравнения теплопроводности (см. листинг 11.7 ниже)
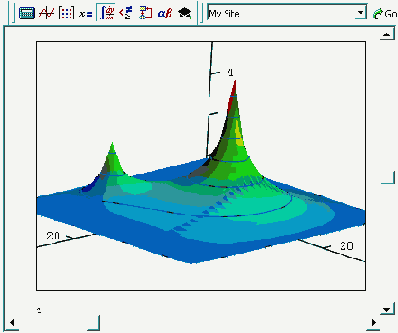
Как несложно сообразить, если искомая функция не зависит от времени, то частная производная по времени в левой части уравнения равна нулю, и само уравнение можно переписать (переобозначив ради упрощения ?<-?/D) следующим образом:
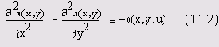
Полученное уравнение, согласно классификации предыдущего раздела, является эллиптическим. Его называют уравнением Пуассона, а для его решения в Matcad предусмотрены две встроенные функции. Если, к тому же, источники равны нулю, то уравнение (11.2), принимающее вид ?u=0, называют уравнением Лапласа.
Одномерное динамическое уравнение
Предположим, что мы рассматриваем задачу распределения тепла не по плоской поверхности, а по удлиненному телу типа металлического стержня (Рисунок 11.3). В этом случае зависимость от координаты у в общем уравнении теплопроводности пропадает, и получается одномерное уравнение:
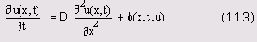
Одномерное уравнение намного проще двумерного, поскольку объем вычислений для реализации алгоритма его численного решения не так велик. Типичное решение одномерного уравнения диффузии тепла с коэффициентом диффузии о=2, нулевым источником ф=о и начальным распределением температуры в форме нагретой центральной области стержня показано (в виде графика поверхности) на Рисунок 11.4.
Начиная с версии Mathcad 11, для решения одномерных параболических и гиперболических уравнений можно применять встроенную функцию pdesolve.