Шаблон неявной схемы для уравнения теплопроводности
Рисунок 11.11. Шаблон неявной схемы для уравнения теплопроводности
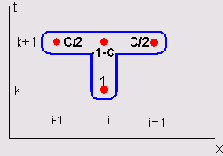
Очень важно, что если само уравнение теплопроводности линейно, то с в левой части разностного уравнения является константой, а ф в его правой части может зависеть только от первой степени и. Поэтому система уравнений (11.10) для всех пространственных узлов 1=1.. .м-l является линейной системой, что существенно упрощает ее решение (поскольку известно, что для линейных систем с ненулевым определителем решение существует и является единственным). Напомним, что для получения замкнутой системы линейных уравнений необходимо дополнить данный набор разностных уравнений граничными условиями, т. е. известными значениями сеточной функции для i=0 и i=M.
Примечание 1
Примечание 1
Если рассматривать нелинейный случай, то на каждом шаге по времени пришлось бы решать систему нелинейных уравнений, число решений которых могло бы быть большим, и среди них требовалось бы отыскать нужное, а не паразитное решение.
Для реализации неявной схемы, таким образом, можно использовать комбинацию средств программирования Mathcad и встроенной функции решения системы линейных уравнений isolve. Один из возможных способов решения предложен в листинге 11.2. Большая часть этого листинга является вводом параметров задачи (шагов, начальных и граничных условий), и только в последней его строке определяется функция пользователя, вычисляющая сеточную функцию на каждом временном слое (при помощи встроенной функции решения системы линейных уравнений isolve). В нескольких предыдущих строках листинга (после расчета коэффициента Куранта сои) формируется матрица системы уравнений А, которая записывается в подходящем для Mathcad виде, как это сделано в листинге 11.2. Как несложно убедиться, столбец правых частей разностных уравнений выражается вычисленными значениями сеточной функции с предыдущего слоя.
Результаты расчетов по неявной схеме показаны на Рисунок 11.12 и, как видно, они дают примерно те же результаты, что и в случае применения явной схемы (см. Рисунок 11.7). Обратите внимание, что решение устойчиво при любых значениях коэффициента Куранта (в том числе и больших 1), поскольку, как следует из соответствующих положений теории численных методов, неявная схема является безусловно-устойчивой.