Расчеты Фурьеспектров гармонических сигналов с разной частотой ("маскировка частот")
Рисунок 14.9. Расчеты Фурье-спектров гармонических сигналов с разной частотой ("маскировка частот")
Избавиться от искажений, вызванных сдвигом ноль-линии, довольно просто. Достаточно (до Фурье-преобразования) вычислить среднее значение выборки и затем вычесть его из каждого элемента выборки. Если после этой операции вычислить Фурье-спектр, то он окажется примерно таким, как показано на Рисунок 14.7.
Маскировка частот
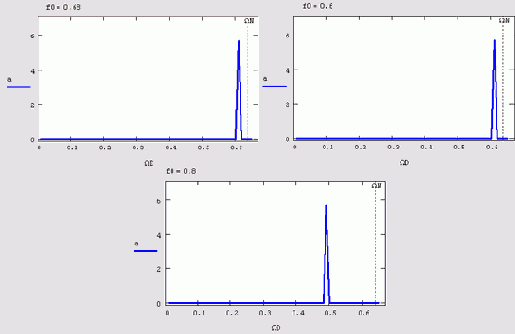
Еще один классический пример ошибочного расчета Фурье-спектра связан с возможным присутствием в сигнале гармоник с частотой, превышающей частоту Найквиста, в данном примере ?N=0.б4 (см. разд. 14.1.Г). Иллюстрация эффекта, называемого "маскировкой частот", приведена на Рисунок 14.9, который содержит расчет спектров трех различных синусоидальных сигналов с разной частотой f0. Первый спектр сигнала с частотой, меньшей частоты Найквиста, вычислен верно, а вот два остальных спектра показывают, что в случае превышения частоты Найквиста в спектре начинают присутствовать "лишние" пики. Появление артефактов спектра связано с тем, что дискретных отсчетов начинает не хватать для того, чтобы прописать высокочастотные гармоники с достаточной информативностью.
Примечание 3
Примечание 3
Напоминаем, что все листинги, имеющиеся в книге, а также документы Mathcad с расчетами всех рисунков, вы найдете на прилагаемом компакт-диске.